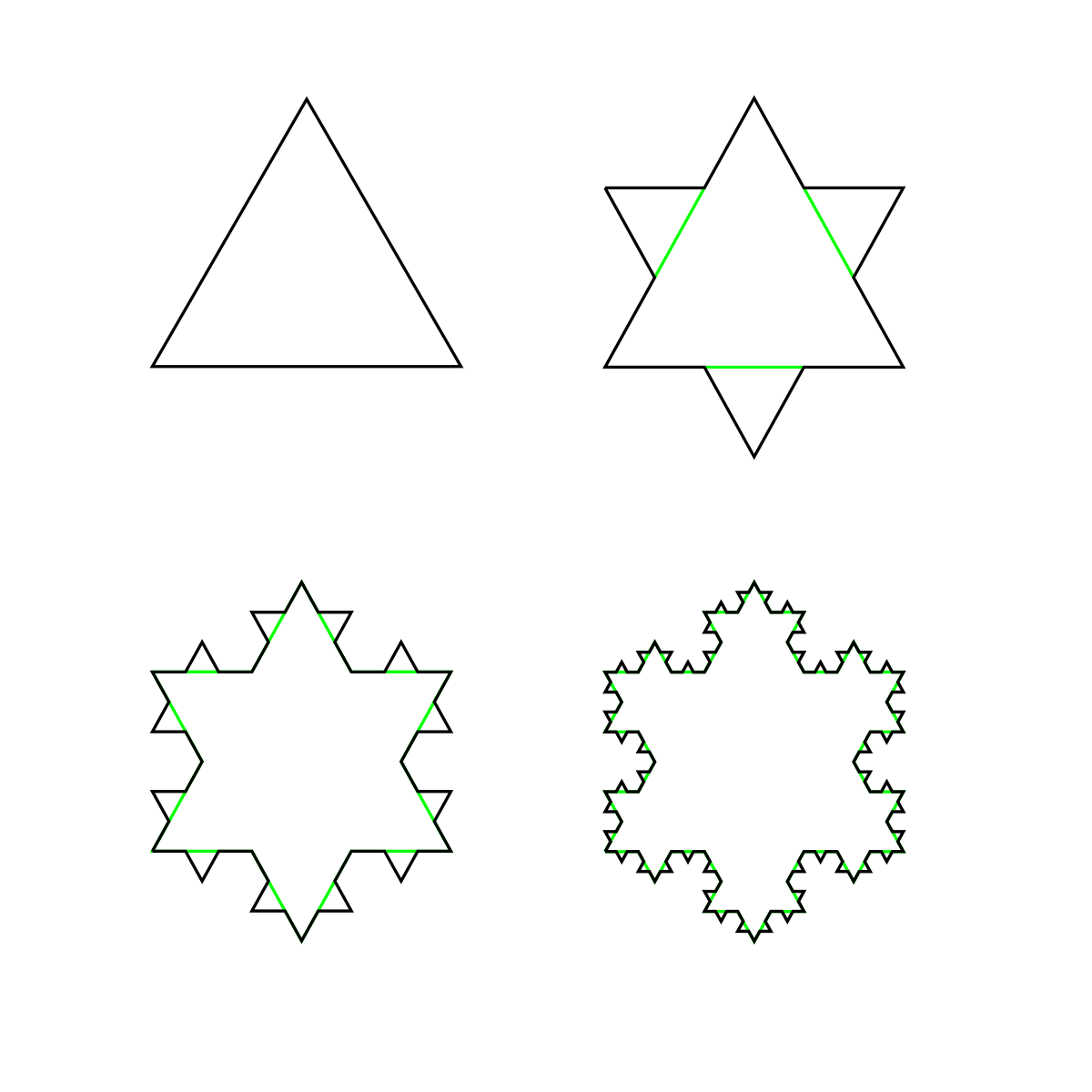
Self Similar Fractals

Two interesting LCHL Patterns questions that are worth trying together are the 2019 Paper 1 Q7 and the 2018 Paper 1 Q9.

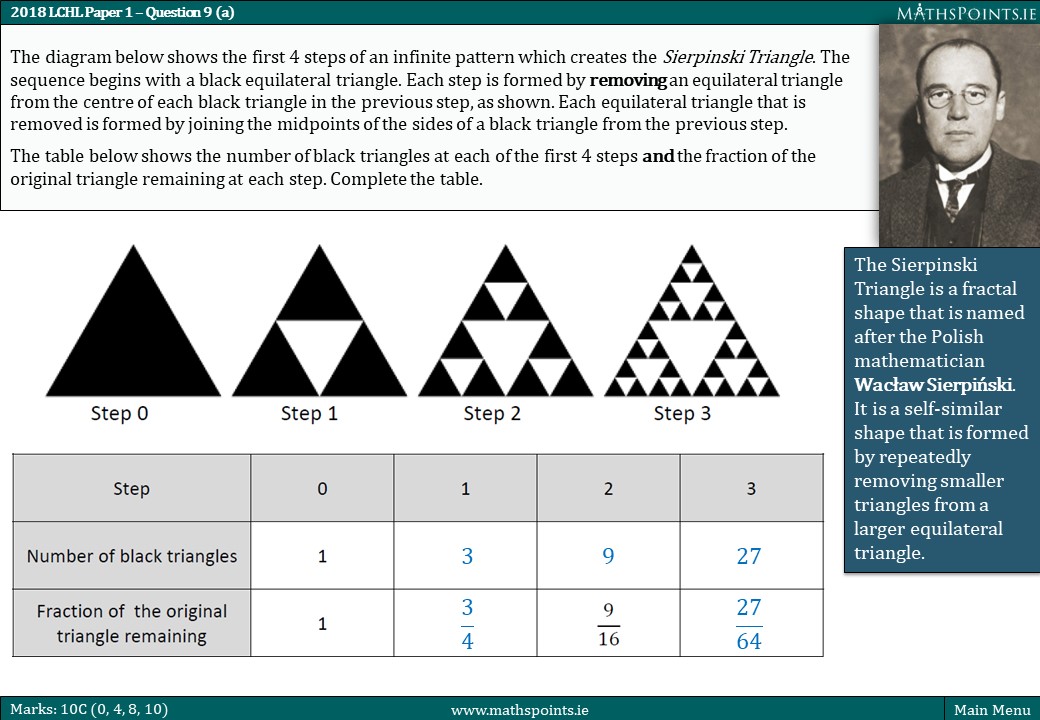
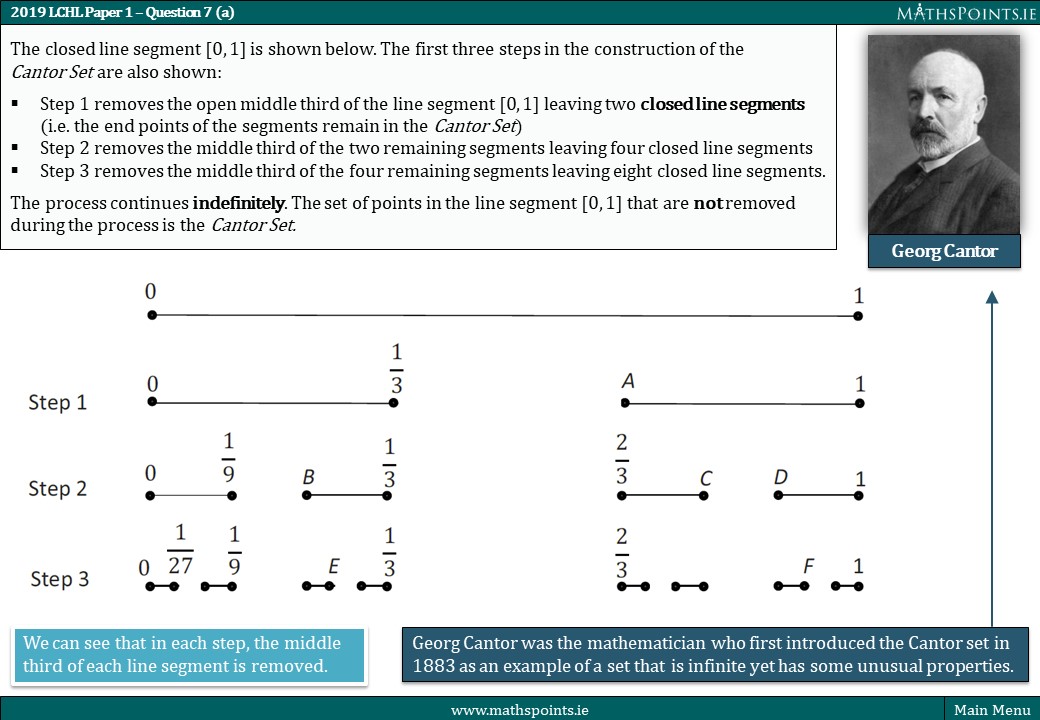
The Cantor Set (2019) and the Sierpinski Triangle (2018) are self similar fractals with very interesting properties.

In the case of the Cantor Set, the construction of the set involves removing the middle third of each line segment repeatedly. At each stage of the construction, the remaining line segments are divided into three equal parts, and the middle segment is removed. This process can be seen as an infinite geometric series, where each term is one-third of the previous term. The sum of this infinite series is equal to one, which means that the Cantor Set contains an infinite number of line segments even though its length is zero.

Similarly, the Sierpinski Triangle can also be seen as a geometric series. The process of constructing the Sierpinski Triangle involves dividing an equilateral triangle into smaller triangles, and then removing the central triangle at each stage of the construction. This process can also be seen as an infinite geometric series, where each term is one-fourth of the previous term. The sum of this infinite series is equal to two-thirds, which means that the Sierpinski Triangle contains an infinite number of smaller triangles even though its area is zero.

These questions can be tough to get into given the time constraints of the exam and I often think this ‘examination through teaching’ is a little unfair…but they are great questions to spent a couple of classes on, in exploring geometric patterns.

Don’t be surprised some day to see a similar question on the Koch snowflake!